(FATEC-SP) - QUESTÃO

Se A = {x| x ∈ Z, -3 < x ≤ 1} e B = {x| x ∈ N, x² < 16}, então (A∪B) - (A∩B) é o conjunto:

Ⓐ {-2, -1 ,0 ,1, 2, 3} 

Ⓑ {-2,-1, 2, 3} 

Ⓒ {-3, -2, -1, 0}

Ⓓ {0, 1, 2, 3}

Ⓔ {0, 1}

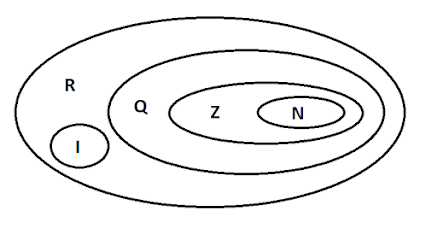
Relembrando conjuntos:

Chamamos de Números Reais o conjunto de elementos representados pela letra maiúscula R, que inclui os:

Números Naturais (N): N = {0, 1, 2, 3, 4, 5,...}

Números Inteiros (Z): Z= {..., -3, -2, -1, 0, 1, 2, 3,...}

Números Racionais (Q): Q = {...,1/2, 3/4, –5/4...}

Números Irracionais (I): I = {...,√2, √3, √7, 3,141592....}

Resolvendo a questão dada temos:

A = {x| x ∈ Z,-3 < x ≤ 1} ⇒ A = {-2, -1, 0, l}

B = {x|x ∈ N, x² < 16} ⇒ B = {0, 1, 2, 3}

(A∪B) = {-2, -1, 0, 1, 2, 3}

(A∩B) = {0, 1}

(A∪B) - (A∩B) = {-2, -1, 0, 1, 2, 3} - {0, 1} = {-2, -1, 2, 3}